Research Article - (2018) Volume 6, Issue 3
The task of solar power forecasting becomes vital to ensure grid constancy and to enable an optimal unit commitment and cost-effective dispatch. Each year latest techniques and approaches appear to increase the exactitude of models with the important goal of reducing uncertainty in the predictions. The aim of the paper is to compile a big part of the knowledge about solar power forcing, to focus on the most recent advancements and future trends. Firstly, the inspiration to achieve an accurate forecast is presented with the analysis of the economic implications it may have. To address the problem superlative prediction models are rummaged by us using machine learning techniques. We make a comparison between multiple regression techniques for creating prediction models, along with linear least squares and support vector machines using multiple kernel functions. Predictions are analyzed by us in our experiments for the day ahead solar radiation data and it is shown that a machine learning approach yields feasible results for short-term solar prediction. The proposed model achieves a root mean square error improvement of around 29% compared to others proposed model except one.
Keywords: Forecasting; Short-term; SVR; Renewable energy; Machine learning
A chief aim of smart grid efforts is to increase the penetration of environmentally-friendly renewable energy sources. The task of solar power forecasting becomes vital to ensure grid constancy and to enable an optimal unit commitment and cost-effective dispatch. The developing focus on renewable energy sources encourages studies concerning the integration of these into existing energy systems. It is expected that solar energy, as well as wind energy, will play a principal role in the future energy supply. Reliable forecast information is required by the fluctuating nature of the energy output from such sources for a successful integration in the electricity grid. To balance the power put into the grid from other sources is the main problem of integrating solar power into the existing electricity grid. The changing output of fossil fuel power plants are increasing as the horizon of the change is decreasing. The total power production and forecasting a requisite to increase the shore of solar power put into the electricity grid can be optimized by improved forecasting of solar power. In the future, solar power forecasting will still be an indispensable tool by Pedar when energy strong techniques are implemented [1].
The methods common in solar forecasting include Numerical weather prediction (NWP) and Model Output Statistics (MOS) to produce forecasts, as well as hybrid techniques that combine ensemble forecasts, and Statistical learning Methods by Tuoy A et al. [2]. The available observation of solar power is the most important input in solar power forecasting up to 2-hours ahead, while for longer horizons NWP model becomes crucial for an accurate forest by Kleissl J [3]. The researcher has placed applying machine learning techniques directly to historical time-series of PV production associated with NWP outcomes among the top models in the last global competition of energy forecasting [4]. Besides it has been presented by the empirical study in Sayeef s and west S that a better accuracy can be yielded by the errors of the solar power forecasting following a non-parametric distribution [5], therefore, using non-parametric models such as machine learning techniques. Support vector machine, a popular tool in machine learning extends support vector Regression. Times series predictions by using SVM including the load forecasting are explored [6]. A good extent explains the SVM utilization in wind forecasting with severe ramp [7]. The prophecy of solar irradiance from SVM and other machine learning methods have been presented in Sharma n et al. [8], it covers that the best forecasts are given by SVM. The aim of the study Silva Fonseca J G et al. is for using SVR to foretell the solar power of a 1-MWPV power plant with the weather variables covering the cloudiness; it shows that the accuracy is being improved by SVR and cloudiness [9]. An approach including support vector machine and weather classification methods to a pv system of 20 kw for a day ahead forecasting is proposed by Shi Jet al. and promising results are shown by the approach [10]. A benchmark study for short-term wind solar power forecasts over different sites in Europe has shown SVM models bring fairly good results [11]. Authority has contrasted two separated models of SVR based on cloud cover to gain more appropriate forecasts of the solar irradiance [12]. A recent review of a dozen of solar power forecasting studies has been presented where the authors specify that the majority of related publishing literature is focusing on solar irradiance in lie of solar power due to the lack of the observed data of the solar power production [13]. An additional step of a conversion to the solar power is needed by the solar irradiance forecast and this might not be as accurate as the direct solar power forecasts. Abuella m and Chowdhury B also uses forecasting solar power [14].
Objectives of the study
• How every prophecy parameter invades each other and the solar strength.
• Sky cover, relative humidity, and cloudburst are extremely interrelated with each other and with solar strength, on the other hand, temperature.
• Formulate models based on linear least squares regression, along with support vector machines (SVM). Regression techniques.
Regression techniques
Linear least squares regression is a simple and generally-used technique to calculate the relationship between a subservient or response variable, e.g., solar intensity and a set of independent variable, or response variable. The sum of the squared differences between the observed solar intensity and the solar intensity predicted by a linear approximation of the forecast weather metrics is minimized by the least squares regression methods. We find a function off that provides appropriate predictions to unseen patterns x′ applying the implemented regression techniques. In the following, we explain linear regression and the basic idea of SVR. First, we focus on linear regression. In this model, Suppose that (x1,y1), (x2, y2), (xn,yn) are realizations of the random variable pairs (X1,Y1),(X2,Y2), (Xn,Yn) . The simple linear regression equation is that the mean of Y is a straight-line function of x. We could write this as: E(Yi)=β0 + β1xi where E(Yi) is used to represent the mean value (expected value) and the subscript i denotes the
Support vector regression
Support vector regression is one of the state-of-the-art techniques for prediction tasks. It is based on support vector machines (SVMs) that were proposed by Vapnik [15]. Kernel trick achieves the binary classes even if they are non-linear, separable in 2-D space, and the trick transforms the classes into a higher dimensional space where the classes become linearly separable. Linear, polynomial, radial basis function is the basic Kernels [16]. The main optimization and the kernel utilized with the SVR forecasting are presented by (1) and (2). For the training of the regressor, we aim at finding weights w by minimizing the following problem, formulated by
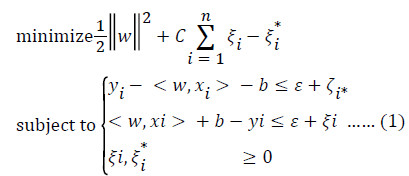
In this formulation, C > 0 as a constant that is used as a parameter that penalizes only those errors that are greater thanε .The so-called slack variables ξi* are introduced to provide a soft margin instead of a hard decision border. To give good results on non-linear separable data as well, kernel functions are used. One can see a kernel function as a similarity measure between pattern and the function is especially useful for non-linear regression tasks.
In our experiments, we employ an RBF-kernel:
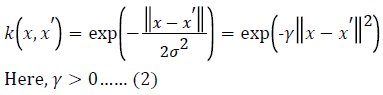
Measures of forecast error
The model that gives the minimum measures of error will be our desired model for forecasting. Suppose for a while that yt is the actual observation and it is the fitted value for the same time period. The following standard statistical measures can be defined if there are in time periods.
The following statistical summary measures of a model’s forecast accuracy are defined using the absolute error.
The Mean Absolute Error (MAE):
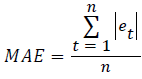
The Root Mean Square Error (RMSE):
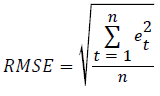
where, et is the forecast error in time period t.
That is,et = ( yˆt − yt ) .
yt is the actual value in the time period t.
n is the number of forecast observations in the estimation period.
The smaller values of MAE and RMSE, the better the model is considered to be.
Collection of data
Extensive traces of historical data are analyzed by us from a weather station, along with the corresponding NWS weather forecasts, to interrelate the weather metrics present in the prophecy with the solar intensity, in watts per m, recorded by the weather station. Both weather prophecy data and observational solar intensity data are collected by us for 10 months starting from January 2012-2015. Historical forecasts data are obtained by us from the NWS at http://www.weather.gov, which we have been collecting for the last 4 years. The solar power plant systems collect local solar power data with two parameters. However, only one of them can be used to predict solar radiation. As the location of collected real daily sunshine and radiation datasets is a flat area at Nadi Airport in Fiji, the main problem is to analyze the amplitude of the solar. There are sunshine and radiation datasets. Each dataset consists of 1435 data samples that are the average values of the solar power in certain duration. It means that totally 4-year solar power data in were recorded from different solar channels in the solar power plant. For long-term forecasting experimental solar radiation data sets are selected and preprocessed, it is prepared for the long-term forecast with a day-ahead horizon.
As it was stated in the introduction, solar power is of great importance in the generation of different kinds of energy. In addition, it is important to propose a model to predict solar power with negligible error and have a better performance compared with reference model – which has a very important place in today's decision making and studies. In the study, we have tried to compare the performance of multiple regression techniques for generating prediction models, including linear least squares and supports vector machines using multiple kernel functions, for long-term prediction of solar power.
From the Figure 1 we can see that overall better prediction performance of RBF-kernel model when kernel parameter γ=0.035 . Table 1 shows the observed and estimated values of different model.
| Observed value | LR | SVML | SVM-RBF-Kernel | SVM-RBF-Kernel | SVM-RBF-Kernel |
|---|---|---|---|---|---|
| (g = 0.01) | (g = 0.02 ) | (g = 0.035 ) | |||
| Estimated | Estimated | Estimated | Estimated | Estimated | |
| 17.8 | 18.98 | 18.42 | 18.67 | 18.72 | 18.88 |
| 18.3 | 15.27 | 16.2 | 18.55 | 18.07 | 18.29 |
| 15.88 | 13.48 | 13.63 | 17.44 | 16.82 | 16.53 |
Table 1: Shows the estimated performance from different models.
From the above table, we say that the estimated value of SVM-RBFKernel ( γ=0.035 ) is better performance than other estimated values although 1-step ahead and 3-step ahead are slightly overestimated 2- step is an almost perfect estimate. For this reason we suggest that SVM-RBF-Kernel ( γ=0.035 ) model is appropriate for long-term prediction of solar radiation data. Figure 2 shows the graphical presentation to compare the observed and estimated value.
From the Figure 1 we can see that overall better prediction performance of RBF-kernel model when kernel parameter γ=0.035. Finally, Table 2 presents the MAE and RMSE value among the different models.
| LR | SVML | SVM-RBF-Kernel | SVM-RBF-Kernel | SVM-RBF-Kernel | |
|---|---|---|---|---|---|
| (g= 0.01 ) | (g= 0.02 ) | (g = 0.035 ) | |||
| MAE | 2.203 | 1.657 | 0.893 | 0.697 | 0.58 |
| RMSE | 2.333 | 1.813 | 1.041 | 0.771 | 0.728 |
Table 2: Shows the MAE and RMSE performance from different models.
From the above table, we say that the MAE and RMSE value of SVM-RBF-Kernel ( γ=0.035 ) is a better performance than other values. For this reason we suggest that SVM-RBF-Kernel ( γ=0.035 ) model is appropriate for short-term prediction of solar radiation data. A root mean square error improvement of around 32% is achieved by the proposed model compared to others proposed reference model except one. All the stages of optimization, training, and testing of the proposed method are done in Weka-3.9.1 software.
At first, we have applied a linear least squares regression method to foretell solar radiation. It is linear least squares regression which is a simple and commonly-used tactic to calculate or response variable.
Linear kernel, a polynomial kernel, and a Radial Basis Function (RBF) kernel. We have found the optimal parameters of the (RBF) kernel to be Y=0.035. The results have shown that the RBF kernel also performs better than the other methods. Moreover, we have given emphasis on the accuracy of prediction models and the source of error. The performances of various models are very difficult to be evaluated, as the existing applications were in different ways. No condition can be perfect by any forecasting model; however, they have served as effective tools to maximize the power captured these increasing the reliability of solar strength to ensure grid constancy and to enable an optimal unit commitment and cost-effective dispatch. We expect that these suggested models are able to provide lots of experience and inspiration from other researchers.
We thank the presidential chair of the University of The Fiji, Dean, School of Science and the chairman of the energy company of Nausori Airports, Nadi in Fiji and funded by the Ministry of Science and Technology, University Grand Commission (UGC), HEQEP, World Bank and Dept. of Statistics, HSTU, Dinajpur. Supporting this work further, we thank the Nausori Airports, Nadi in Fiji for providing the wind data set.